Problem Set 4

Due by 11:59 p.m. Eastern time on July 28, 2026.
See below for a summary of the policies regarding late submissions.

Preliminaries

Homework is due by 11:59 p.m. Eastern time on the stated due date. If it is submitted more than 10 minutes after that time, it will be considered a full day late. There will be a 10% deduction for submissions that are up to one day late, and a 20% deduction for submissions that are 2 or 3 days late. We will not accept any homework that is more than 3 days late. Plan your time carefully, and don’t wait until the last minute to begin an assignment. Starting early will give you ample time to ask questions and obtain assistance.

In your work on this assignment, make sure to abide by our policies on academic conduct.

If you have questions while working on this assignment, please come to office hours, post them on Ed Discussion, or email cscie22-staff@lists.fas.harvard.edu

Part I

50 points total

Creating the necessary folder

Create a subfolder called ps4 within your s22 folder, and put all of the files for this assignment in that folder.

Creating the necessary file

The problems from Part I will all be completed in a single PDF file. To create it, you should do the following:

1. Access the template that we have created by clicking on this link and signing into your Google account as needed.

2. When asked, click on the Make a copy button, which will save a copy of the template file to your Google Drive.

3. Select File->Rename, and change the name of the file to ps4_partI.

4. Add your work for the problems from Part I to this file.

5. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file on your machine. The resulting PDF file (ps4_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1 Tree traversal puzzles

10 points total; 5 points each part

1. When a binary tree of characters (which is not a binary search tree) is listed in postorder, the result is IKHAFLMBCQ. Inorder traversal gives IAKHQCFLBM. Construct the tree by editing the diagram that we have provided in section 1-1 of ps4_partI:

   • Click on the diagram and then click the Edit link that appears below the diagram.

   • We have provided the necessary nodes and edges, but you will need to move them into the appropriate positions and connect them.

   • When you have completed your edits, click the Save & Close button.

2. When a binary tree of characters (which is not a binary search tree) is listed in preorder, the result is BAFCIDGEHJ. Inorder traversal gives FCAIBGHEJD. Construct the tree by editing the diagram that we have provided in section 1-2 of ps4_partI.

Problem 2 Huffman encoding

8 points total

Consider the following table of character frequencies:

1. (6 points) Show the Huffman tree that would be constructed from these character frequencies by editing the diagram that we have provided in section 2-1 of ps4_partI. It includes some of the necessary nodes and edges, but you should create more of them as needed, move them into the appropriate positions, and connect them.

2. (2 points) Using the Huffman tree from part 1, what will be the encoding of the string field?

Problem 3 Binary search trees

10 points; 2 points each part

Consider the following binary search tree, in which the nodes have the specified integers as keys:

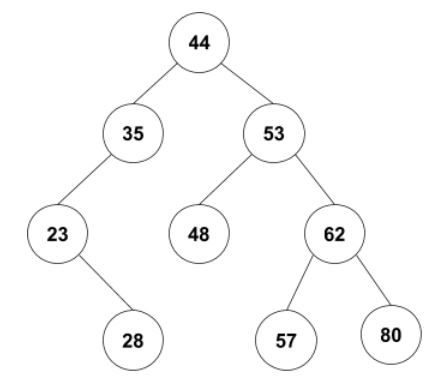
1. If a postorder traversal were used to print the keys, what would the output be?

2. What would be the output of a preorder traversal?

We will cover the material needed for the remaining parts of this problem in the July 20 lecture.

3. Show the tree as it will appear if 33 is inserted, followed by 60. Edit the diagram that we have provided in section 3-3 of ps4_partI.

4. Suppose we have the original tree and that 42 is deleted and then 26 is deleted, using the algorithm from the lecture notes. Show the final tree by editing the diagram that we have provided in section 3-4 of ps4_partI.

5. Is the original tree balanced? Explain briefly why or why not.

Problem 4 Checking for keys below a value

12 points total

The code below represents one algorithm for determining if there are any keys smaller than a given value v in an instance of our LinkedTree class. The anySmallerInTree() method returns true if there are any keys smaller than v in the tree/subtree whose root node is specified by the first parameter of the method, and it returns false if there are no such keys. The anySmaller() method returns true if there are any keys smaller than v in the entire tree represented by the LinkedTree object on which the method is invoked, and false otherwise.

public boolean anySmaller(int v) {
    // make the first call to the recursive method,
    // passing in the root of the tree as a whole
    return anySmallerInTree(root, v);
}

private static boolean anySmallerInTree(Node root, int v) {
    if (root == null) {    
        return false;
    } else {
        boolean anySmallerInLeft = anySmallerInTree(root.left, v);
        boolean anySmallerInRight = anySmallerInTree(root.right, v);
        return (root.key < v || anySmallerInLeft || anySmallerInRight);
    }
}

1. For a binary tree with n nodes, what is the time efficiency of this algorithm as a function of n? Use big-O notation, and explain your answer briefly.

   If the time efficiency depends on the keys in the tree or on the tree’s shape, you should explain why and give three big-O expressions: one for the best case, one for the worst case if the tree is balanced, and one for the worst case if the tree is not balanced. If the time efficiency does not depend on the keys or the shape of the tree, you should explain why and give one big-O expression.

2. If the tree is a binary search tree, we can revise the algorithm to take advantage of the ways in which the keys are arranged in the tree. Write a revised version of anySmallerInTree that does so. Your new method should avoid visiting nodes unnecessarily. In the same way that the search for a key doesn’t consider every node in the tree, your method should avoid considering subtrees that aren’t needed to determine the correct return value. Like the original version of the method above, your revised method should also be recursive.

   Note: In the files that we’ve given you for Part II, the LinkedTree class includes the methods shown above. Feel free to replace the original anySmallerInTree() method with your new version so that you can test its correctness. However, your new version of the method should ultimately be included in your copy of ps4_partI.

3. For a binary search tree with n nodes, what is the time efficiency of your revised algorithm as a function of n?

   Here again, if the time efficiency depends on the keys in the tree or on the tree’s shape, you should explain why and give three big-O expressions: one for the best case, one for the worst case if the tree is balanced, and one for the worst case if the tree is not balanced. If the time efficiency does not depend on the keys or the shape of the tree, you should explain why and give one big-O expression.

Problem 5 2-3 Trees and B-trees

10 points; 5 points each part

Let’s say that you want to insert items with the following sequence of keys:

F, C, H, I, E, J, A, D, P, M 

1. Insert this sequence into an initially empty 2-3 tree by editing the diagram that we have provided in section 5-1 of ps4_partI. Show the tree after each insertion that causes a split of one or more nodes, and the final tree.

   We have given you a sample diagram that includes nodes of different sizes. Make copies of the diagram so that you can use separate diagrams for the results of each insertion that causes a split, and for the final tree. Note that you do not need to keep the shape of the tree that we have given you. Rather, you should edit it as needed: deleting or adding nodes and edges, replacing the Xs with keys, adding or removing keys, and making whatever other changes are needed.

2. Insert this sequence into an initially empty B-tree of order 2 by editing the diagram that we have provided in section 5-2 of ps4_partI. Show the tree after each insertion that causes a split of one or more nodes, and the final tree. Here again, you should make copies of the diagram that we have given you and edit them as needed.

Submitting your work for Part I

Submit your ps4_partI.pdf file by taking the following steps:

1. If you still need to create a PDF file, open your file on Google Drive, choose File->Download->PDF document, and save the PDF file on your machine.

2. Click on the name of the assignment in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

4. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

5. Once you have assigned pages to all of the problems in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

50-60 points total

Preparing for Part II

1. You should begin by downloading the following zip file:
   ps4_partII.zip

2. Unzip/extract the contents of the file.

3. Depending on your system, after extracting the contents you will either have:

   • a folder named ps4_partII that contains all of the files that you need for the problems in Part II

   • an outer folder called ps4_partII that contains an inner folder named ps4_partII that contains all of the Java files that you need.

   Take the ps4_partII folder that actually contains the necessary files and drag it into your ps4 folder so that you can easily find and open it from within VSCodium.

4. Launch VSCodium on your laptop.

5. In VSCodium, select the File->Open Folder menu option, and use the resulting dialog box to find and open the ps4_partII folder that you created above – the one that contains the provided files. (Note: You must open the folder; it is not sufficient to simply open one of the Java files in the folder.)

   The name of the folder should appear in the Explorer pane on the left-hand side of the VSCodium window, along with a list of all of its contents.

We will cover material relevant to Part II in lecture on July 20.

Problem 6 Adding methods to the LinkedTree class

25 points

Make sure to begin by following the instructions given above in the Preparing for Part II section.

In the file LinkedTree.java, add code to the LinkedTree class that completes the following tasks:

1. Write a non-static sumKeysTo(int key) method that takes takes an integer key as its only parameter and that uses uses iteration to determine and return the sum of the keys on the path from the root node to the node with the specified key, including the key itself. Your method should take advantage of the fact that the tree is a binary search tree, and it should avoid considering subtrees that couldn’t contain the specified key. It should return 0 if the specified key is not found in the tree.

   Note: There are two methods in the LinkedTree class that can facilitate your testing of this method and the other methods that you’ll write:

   • The insertKeys() method takes an array of integer keys, and it processes the array from left to right, adding a node for each key to the tree using the insert() method. (The data associated with each key is a string based on the key, although our tests will focus on just the keys.)

   • The levelOrderPrint() method performs a level-order traversal of the tree and prints the nodes as they are visited; each level is printed on a separate line. This method doesn’t show you the precise shape of the tree or the edges between nodes, but it gives you some sense of where the nodes are found.

   For example, below are some examples of depthIter(). To help you visualize the tree, it’s worth noting that we’re using an array of keys that produces the following binary tree: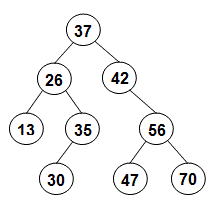

   

   If we run the following test code:

   LinkedTree tree = new LinkedTree();
   System.out.println("sum 1 = " + tree.sumKeysTo(13));
   int[] keys = {37, 26, 42, 13, 35, 56, 30, 47, 70};
   tree.insertKeys(keys);
   System.out.println("sum 2 = " + tree.sumKeysTo(13));
   System.out.println("sum 3 = " + tree.sumKeysTo(56));
   System.out.println("sum 4 = " + tree.sumKeysTo(37));
   System.out.println("sum 5 = " + tree.sumKeysTo(50));
   

   we should see:

   sum 1 = 0
   sum 2 = 76
   sum 3 = 135
   sum 4 = 37
   sum 5 = 0
   

2. Write two methods that together allow a client to determine the number of leaf nodes in the tree:

   • a private static method called numLeafNodesInTree() that takes a reference to a Node object as its only parameter; it should use recursion to find and return the number of leaf nodes in the binary search tree or subtree whose root node is specified by the parameter. Make sure that your method correctly handles empty trees/subtrees – i.e., cases in which the value of the parameter root is null.

   • a public non-static method called numLeafNodes() that takes no parameters and that returns the number of leaf nodes in the entire tree. This method should serve as a “wrapper” method for numLeafNodesInTree(). It should make the initial call to that method – passing in the root of the tree as a whole – and it should return whatever value that method returns.

   For example, if we run the following tests, which use the same keys array as the one given above:

   LinkedTree tree2 = new LinkedTree();
   System.out.println("count 1 = " + tree2.numLeafNodes());
   int[] keys = {37, 26, 42, 13, 35, 56, 30, 47, 70};
   tree2.insertKeys(keys);
   System.out.println("count 2 = " + tree2.numLeafNodes());
   

   we should see:

   count 1 = 0
   count 2 = 4
   

3. Write a non-static method deleteSmallest() that takes no parameters and that uses iteration to find and delete the node containing the smallest key in the tree; it should also return the value of the key whose node was deleted. If the tree is empty when the method is called, the method should return -1. Your method should take advantage of the fact that the tree is a binary search tree.

   Important: Your deleteSmallest() method may not call any of the other LinkedTree methods (including the delete() method), and it may not use any helper methods. Rather, this method must take all of the necessary steps on its own – including correctly handling any child that the smallest node may have.

   For example, if we run the following tests using the same keys array as above:

   LinkedTree tree3 = new LinkedTree();
   System.out.println("empty tree: " + tree3.deleteSmallest());
   
   int[] keys = {37, 26, 42, 13, 35, 56, 30, 47, 70};
   tree3.insertKeys(keys);
   System.out.println("levels of original tree:");
   tree3.levelOrderPrint();
   
   System.out.println("\ndeleteSmallest: " + tree3.deleteSmallest());
   tree3.levelOrderPrint();
   System.out.println("\ndeleteSmallest: " + tree3.deleteSmallest());
   tree3.levelOrderPrint();
   

   we should see:

   empty tree: -1
   levels of original tree:
   37
   26 42
   13 35 56
   30 47 70
   
   deleteSmallest: 13
   37
   26 42
   35 56
   30 47 70
   
   deleteSmallest: 26
   37
   35 42
   30 56
   47 70
   

   Note that first we delete 13, because it is the smallest key in the original tree. Next we delete 26, because it is the smallest remaining key. As a result of these deletions, 35 and 30 move up a level in the tree.

4. Writing well-formatted units tests is an extremely important part of a programmer’s work. In the main() method of LinkedTree.java, we’ve given you an example of what such a unit test should look like.

   Update the main() method to include at least two unit tests for each of your new methods. Your unit tests must follow the same format as our example test. In particular, the output of each of your unit tests should include:

   • a header that specifies the test number and a description of what is being tested
   • the actual return value that you get from that test
   • the expected return value
   • whether the actual return value matches the expected return value.

   Put each test in the context of a try-catch block so that you can handle any exceptions that are thrown. Leave a blank line between tests.

   Additional notes:

   • For part 2 (numLeafNodesInTree()/numLeafNodes()), your unit tests only need to call numLeafNodes(), since doing so will also call numLeafNodesInTree().

   • Our model unit test can be used to test the anySmaller()/anySmallerInTree() methods from Problem 4.

Problem 7 Binary tree iterator

25 points

We will cover material that will be helpful for this problem in section.

The traversal methods that are part of the LinkedTree class are limited in two significant ways: (1) they always traverse the entire tree; and (2) the only functionality that they support is printing the keys in the nodes. Ideally, we would like to allow the users of the class to traverse only a portion of the tree, and to perform different types of functionality during the traversal. For example, users might want to compute the sum of all of the keys in the tree. In this problem, you will add support for more flexible tree traversals by implementing an iterator for our LinkedTree class.

You should use an inner class to implement the iterator, and it should implement the following interface:

public interface LinkedTreeIterator {
    // Are there other nodes to see in this traversal?
    boolean hasNext();

    // Return the value of the key in the next node in the
    // traversal, and advance the position of the iterator.
    int next();
}

There are a number of types of binary-tree iterators that we could implement. We have given you the implementation of a preorder iterator (the inner class PreorderIterator), and you will implement an postorder iterator for this problem.

Your postorder iterator class should implement the hasNext() and next() methods so that, given a reference named tree to an arbitrary LinkedTree object, the following code will perform a complete postorder traversal of the corresponding tree:

LinkedTreeIterator iter = tree.postorderIterator();
while (iter.hasNext()) {
    int key = iter.next();

    // do something with key
}

Here are the tasks that you should perform:

0. In order for an iterator to work, it’s necessary for each node to maintain a reference to its parent in the tree. These parent references will allow the iterator to work its way back up the tree.

   The version of LinkedTree that we discussed in lecture did not include parent references, but we’ve included them in the copy of LinkedTree.java that we’ve given you for this assignment, and it is important that you start by reviewing the code that we’ve added for this purpose:

   1. First, note that we have added a field called parent to the inner Node class:

      private class Node {
          private int key;    
          private LLList data;
          private Node left;
          private Node right;
          private Node parent;     // added for PS 4, Problem 7
          ...
      

      This new parent field is assigned a value of null by the Node constructor. It doesn’t actually point to the node’s parent until the Node object is added to the tree by the insert method.

   2. As discussed in lecture, the insert method makes use of a local variable named parent that serves as a trailing reference during the search for the key that is being inserted. At the end of that search, the local variable parent holds a reference to the Node object that is about to become the parent of the new node. As a result, we are able to set the value of the new node’s parent field by using the following line of code at the very end of the insert method:

      newNode.parent = parent;
      

      Note: When we insert an item into an empty tree, the local variable parent will be null at the end of the insert method, and thus we will end up assigning null to newNode.parent. This makes sense, because when we add a node to an empty tree, it becomes the root of the entire tree, and thus its parent field should have a value of null!

   3. When a node that has one child is deleted, that child’s parent changes. This change is handled by the following lines, which have been added to the middle of the deleteNode method:

      if (toDeleteChild != null) {
          toDeleteChild.parent = parent;
      }
      

1. The deleteMax method that you implemented for Problem 6 can also change the parent of a node in some cases. Update your deleteMax method so that it correctly updates the parent field of the affected Node object in such cases.

2. Review the code that we’ve given you in the PreorderIterator class and the preorderIterator() method, and understand how that iterator works. We will review this iterator in section, and we have also provided an overview of it here.

3. Next, add a skeleton for your iterator class, which you should name PostorderIterator (note that only the P and I are capitalized). It should be a private inner class of the LinkedTree class, and it should implement the LinkedTreeIterator interface. Include whatever private fields will be needed to keep track of the location of the iterator. Use our PreorderIterator class as a model.

4. Implement the constructor for your iterator class. Make sure that it performs whatever initialization is necessary to prepare for the initial calls to hasNext() and next().

   In the PreorderIterator constructor that we’ve given you, this initialization is easy, because the first node that a preorder iterator visits is the root of the tree as a whole. For an postorder iterator, however, the first node visited is not necessarily the root of the tree as a whole, and thus you will need to perform whatever steps are needed to find the first node that the postorder iterator should visit, and initialize the iterator’s field(s) accordingly.

5. Implement the hasNext() method in your iterator class. Remember that it should execute in O(1) time.

6. Implement the next() method in your iterator class. Make sure that it includes support for situations in which it is necessary to follow one or more parent links back up the tree, as well as situations in which there are no additional nodes to visit. If the user calls the next() method when there are no remaining nodes to visit, the method should throw a NoSuchElementException.

7. Add an postorderIterator() method to the outer LinkedTree class. It should take no parameters, and it should have a return type of LinkedTreeIterator. It should create and return an instance of your new class.

8. Test everything! At a minimum, you must do the following: In the main() method, add a unit test that uses the while-loop template shown near the start of this problem to perform a full postorder traversal of a sample tree.

Problem 8 Finding keys between two values

10 points; required for grad credit; partial extra credit for others

In your LinkedTree class, add two methods that together allow a client to find and print all keys in a binary search tree that are between two boundary values:

• a method with the following header:

  private static void findBetweenInTree(Node root, int k1, int k2)
  

  It should process the tree or subtree whose root is specified by the parameter root, finding and printing all keys in that tree/subtree that are between k1 and k2 inclusive (i.e., all keys greater than or equal to k1 and less than or equal to k2). The relevant keys should be printed in increasing order, separated by spaces. See the important notes below for some additional guidelines.

• a public non-static method called findBetween() that serves as a “wrapper” method for your private static method. It should take two integers k1 and k2, and it should begin by checking those parameters, throwing an IllegalArgumentException if k1 is greater than k2. Otherwise, it should make the initial call to findBetweenInTree – passing in the root of the tree as a whole as the first parameter.

For example, if we run the following test:

LinkedTree tree = new LinkedTree();
int[] keys = {37, 26, 42, 13, 35, 56, 30, 47, 70};
tree.insertKeys(keys);
tree.findBetween(30, 50);

we should see:

30 35 37 42 47

Important notes

• For full credit, your static method must take full advantage of the fact that the tree is a binary search tree, and it should avoid considering subtrees that could not contain any keys between k1 and k2.

• Make sure that your static method correctly handles empty trees/subtrees – i.e., cases in which the value of the parameter root is null. For such cases, it should simply return without printing anything.

Submitting your work for Part II

You should only submit your LinkedTree.java file.

Here are the steps:

1. Click on the name of the assignment in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

2. Add the file to the box labeled DRAG & DROP. You can either drag and drop the file from its folder into the box, or you can click on the box itself and browse for the file.

3. Click the Upload button.

4. You should see a box saying that your submission was successful. Click the (x) button to close that box.

5. The Autograder will perform some tests on your file. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

6. If needed, use the Resubmit button at the bottom of the page to resubmit your work. ** Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.**

7. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that you see the code that you want us to grade.